کرونکر در جایی گفته بود که ایزد اعداد طبیعی را خلق کرده اما سایر اعداد همگی مخلوقات بشر هستند. این حرف (فارغ از شوخی عقیدتی مستتر در آن) به درجات زیادی در رابطه با اعضاء اولیه ی مجموعه ی اعداد ناتورال (طبیعی) صحیح است. برخی از ریاضیدانان صفر را جزئی از اعداد طبیعی قلمداد می کنند و برخی دیگر خیر. من نیز مایلم که صفر را جزئی از اعداد طبیعی بدانم.
بگمان من اعداد صفر، یک و دو مهمترین اعدادی هستند که ساخت هر عدد دیگری بمدد آن ها رخ می دهد. درک آدمی از این اعداد تا حد زیادی ریشه در قوانین حاکم بر مجموعه ی مغز – ذهن – روان وی دارد. جالب است بدانیم که مطالعات انجام گرفته در حوزه ی رفتارشناسی جانوری نیز نشان می دهند که سایر موجودات به درصد زیادی با آدمی در این درک سهیم بوده و با گونه ی ما دارای اشتراکات فراوانی می باشند. درک از عدد (number sense) یعنی اینکه ما بتوانیم بین چیزها با کمیت های مختلف از نظر بزرگی و یا کوچکی آن کمیت، فرق قایل شویم (افتراق هایی که خود را در زبان آدمی نیز متجلی ساخته اند).
دستور زبان سامی عربی، بشکل بدوی، چیزها را به دسته های مفرد، مثنی و جمع تقسیم می کند. ریشه ی لغوی عدد 3 در بسیاری از زبان ها از ریشه ی “خیلی” است. دستور زبان های هندواروپایی تا حد بسیار زیادی، بشکل صحیح تر، چیزها را به دو دسته ی مفرد و جمع تقسیم بندی کرده است و این یعنی اینکه یا چیزها منفرد هستند (عدد 1) و یا اینکه جمع هستند (مثلا عدد 2) و هر چیزی از نظر کمی مادونِ آن (عدد صفر / نبودن) و ماورایِ آن (مثلا عدد 3) صرفا جمعی بزرگ تر است. این مسایل به خوبی نشان می دهند که گویا مفاهیم نبودن (صفر)، بودنِ منفرد (یک) و بودنِ چندگانه (دو و غیره) همگی مشترکاتی بنیادین بین موجودات مغزمند هستند (رجوع شود به ابتدای کتاب “عدد، زبان علم” نوشته ی توبیاس دانتسیگ).
اگرچه رسیدن به توجیهی منطقی – فلسفی برای اعداد ناتورال، کار ساده ایست اما دست پیدا کردن به همین دست توجیهات برای سایر اقسام اعداد کار چندان راحتی نیست. نکته ی جالب توجه این است که تمامی اعداد عجیب و غریب (مثل اعداد گنگ) را از همین اعداد ناتورال می سازیم. طول قطر یک مربع با ضلع یک، عدد رادیکال دو است که عددی گنگ می باشد. این یعنی اینکه نشان دادن این عدد چونان کسری از دو عدد صحیح ممکن نیست.
در نظریه ی ریاضیات طبیعی براحتی می توان ساختار مجموعه ای اعداد ناتورال را پیدا کرد. اگر همه ی اعداد از این اعداد ناتورال ساخته می گردند، پس می بایست که بتوان ساختاری مجموعه ای برای آنها پیدا نمود. یکی از پرسش های پیش رو این نظریه به دست دادن ساز و کاری برای پیدا کردن مجموعه های ما به ازای اعداد غیرناتورال است. به گمان من این اعداد می بایست با کسر و اضافه ی مجموعه ی فی (تهی) از مجموعه های ناتورال ساخته شوند. این مسئله آدمی را به یاد مسئله ی ژنتیک اعداد می اندازد. گویا هر عددی دارای یک تبار ژنتیکی است. اعداد غیرناتورال اعدادی با نقشه های ژنتیکی جهش یافته هستند. نقشه ی ژنتیکی هر عدد نشان خواهد داد که این عدد از کجا حاصل شده و یا اینکه نسل های بعدی آن چه خواهند بود.
باز بعبارت دیگر، این ژنوم عددشناختی در اولین سطح نشان خواهد داد که والد (و یا والدین) عدد مزبور چه عددی (و یا اعدادی) می باشد (و یا می باشند) و در سطوح بعدی فرزندان این عدد چه خواهند بود. بعنوان مثال عدد 3/2 از دو عدد طبیعی 2 و 3 ساخته می شود. این عدد یعنی اینکه عدد 2 به 3 واحد تقسیم گردد. طبق حسابی که (متاثر از فرگه) قبلا در این نظریه ارایه شده است، عدد 2 در انبان ژنتیکی خود دارای دو تهی و عدد 3 دارای چهار تهی است. وقتی می خواهیم آن ها را بر هم تقسیم کنیم، خطی کسری خواهیم داشت که در صورت و مخرج آن به ترتیب 2 و 4 مجموعه ی تهی بدین شکل بر روی هم سوار می شوند:
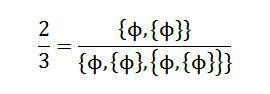
تقسیم 2 به 3 قسمت از نگرگاه نظریه ی مجموعه ها، ما را با چنین حالتی مواجه می سازد. اکنون پرسش پیش رو ما، پیدا نمودن الگوریتمی برای این قسم تقسیم هاست. اگر بخواهیم به این حساب بشکل کلاسیک نگاه کنیم، می توانیم مجموعه ی بالا را با بخشی از مجموعه ی پایین ساده کرده و در اثر یک فاکتورگیری ساده به عدد “یک دوم” برسیم که البته ارتباطی با “دو سوم” مربوطه ندارد. پس چگونه حرکتی می تواند از منظر حسابی نظریه ی مجموعه هایی این وضعیت را برای ما حل و فصل کند.
با چه مجموعه ای می توان “دو سوم” را نشان داد؟ آیا برای نشان دادن آن کافی است که به کسر نظریه ی مجموعه هایی فوق بسنده کنیم و یا اینکه می بایست خروجی آن را بشکل یک مجموعه ی واحد نشان دهیم، دقیقا به همان طریقی که می توان “دو سوم” را بشکل تک عدد “شصت و شش صدم” (که عملا اعشاری تا انتهای دنیاست) نشان داد. پس همانطور که در بالا اشاره شد، اولین گام در راستای ادامه ی موفقیت آمیز نظریه ی ریاضیات طبیعی، پیدا کردن الگوریتمی برای ساختن مجموعه هایی معرف اعداد غیرناتورال می باشد.

در مورد اين جمله:
“بگمان من اعداد صفر، یک و دو مهمترین اعدادی هستند که ساخت هر عدد دیگری بمدد آن ها رخ می دهد. ”
چند ابهام براي من پيش آمده است:
اگر نام طبيعي روي مجموعه اعداد مي گذاريم چون در طبيعت عدد صفر نيست پس نبايد جزو اين مجموعه باشد البته مي توان نام ديگري روي اين مجموعه نهاد كه گويا اعداد حسابي به آن مي گويند.
دوم اينكه همه اعداد مي توانند از اعداد صفر و يك حاصل شوند با جمع يك با خودش مي توانيم به “عدد دو” برسيم پس چرا شما “عدد دو” را نيز در جمله تان آورده ايد؟